끄적끄적

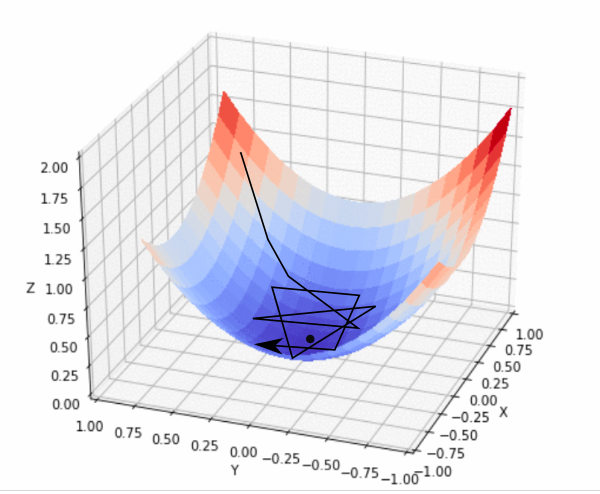
Generalization

Generalization의 필요성

 머신러닝에서 학습은 Train Loss를 줄이는 방향으로 진행된다. 하지만 우리가 원하는 것은 Training data에 대한 손실을 최소화하는 것이 아니라, 앞으로 우리의 모델이 마주하게 될 본적 없는 새로운 데이터를 잘 분류하는 것이고, 이를 위해 우리는 우리의 모델을 일반화(Generalization)해야 한다.

 즉, 모델이 Training data에 너무 맞춰지면 본적 없는 데이터에 제대로 대처하지 못한다.

방법

1. 차원을 줄인다.

 필요없는 input feature를 줄임으로써 우리의 모델이 너무 커지는 것(Training data에 민감해지는 것)을 방지한다.

2. Regularize

 $w$의 크기가 너무 커지지 않도록 한다. 전 강의에서 학습한 Gradient Descent를 예로 들면, 일반적으로 $\lvert \vec{w} \rvert$ 는 학습이 진행됨에 따라 커지는데, TrainLoss 이외에도 $\lvert \vec{w} \rvert$ 에 대한 제약을 줌으로써 $w$의 크기를 조절한다. ($min_\vec{w} (TrainLoss(\vec{w}) + \frac{\lambda}{2} \lvert \vec{w} \rvert^2)$)

 Gradient Descent는 다음과 같이 진행한다.

 $\vec{w} = \vec{w} - \eta(\triangledown_\vec{w} Loss(\vec{w,y,w}) + \lambda \lvert \vec{w} \rvert) $

 이러한 방식을 L2 Regularization이라 한다.

3. Training data로 부터 일부를 떼어 Validation data로 활용한다.

 Test data를 활용하지 않으면서, 새로운 데이터에 대한 반응을 보기 위하여 Training data 중 일부를 떼어 Validation data로 활용한다.

K mean clustering

Unsupervised learning

 보통 라벨링된 데이터는 구하기 매우 힘들다. 또한 데이터들은 그 자체로 여러가지 특징들을 가지고 있는데, 이러한 특징들을 자동적으로 찾아 분류하는 방법이다.

K mean clustering

 데이터들을 K개의 cluster로 묶는 방법이며, 각 데이터 $\phi(x)$를 cluster $k$의 centroid인 $\mu_k$ 중 centroid가 가장 가까운 cluster에 배정하는 방식이다. 이때 손실이 최소화되는 centroid의 위치를 찾는 방식으로 진행된다. 손실함수는 다음과 같이 모든 data로부터 소속된 cluster의 centroid까지의 거리의 합으로 정의한다.

 $Loss_{kmeans}(z,\mu) = \sum_i \lvert \phi(x) - \mu_{z_i} \rvert ^2$

Python Code

 먼저 클러스터링에 필요한 함수들을 정의합니다.

 클러스터의 개수는 2개로 고정하기로하고, 클러스터들의 첫 centroid는 램덤으로 주게되는데, 여기서는 편의상 (6,0)과 (0,6)으로 하겠습니다. 그러면 각 sample들은 색깔로 표시한 것과 같이 클러스터링 되게 됩니다. 여기까지가 아래 코드의 line4까지가 됩니다. 첫 그림에서는 $y=x$ 그래프를 기준으로 위 아래로 나누어진것을 확인할 수 있습니다.

 line6부터는 새로 할당된 클러스터들에 대하여 centroid를 다시 계산하고 이전의 에러보다 현재의 에러가 작은 경우, 바뀐 centroid를 채택하고 cluster를 다시 배정하게 됩니다.

* K-means 알고리즘에서 중요한 것은, K-means 알고리즘은 항상 local minimum에 도달하긴 하지만, 그곳이 global minimum이라는 보장은 없으며, 초기조건을 바꾸어가며 가장 적절한 centroid들을 찾아야 합니다.

Reference

Stanford CS221 Lecture4

Gradient Discent

 어떤 함수 $f(x)$가 있을 때, $f(x)$가 최소가 되는 $x$ 값을 찾는 방법으로, $f(x)$의 gradient의 반대방향으로 $x$값을 변화시키는 방법이다. (gradient의 방향이 $f(x)$를 최대화시키는 방향을 나타내는데, 우리는 $f(x)$가 최소가 되는 $x$값을 찾고 싶으므로 반대방향으로 움직여야 한다.)

Linear Regression

 Feature $\phi(x)$로 부터 $y$를 예측하는 선형회귀 모델에서 input $x$로부터의 예측값 $f_w(x)$는 다음과 같이 주어진다.

 $f_w(x) = \vec{w} \cdot \phi(x)$

출처 : https://blog.paperspace.com/content/images/2018/05/fastlr.png

 위의 그림은, $z$ 값이 $f_w(x)$가 되며, $x$가 2차원으로 $(x,y)$로 주어지는 경우로, 우리는 점이 찍혀있는 $f_w(x)$ 값이 가장 낮은 점의 $(x,y)$값을 찾기를 원하는 것이다.

Loss

 본강의에서는 Loss를 위의 예측값과 실제 값 $y$의 차의 제곱, 즉 residual의 제곱으로 한다. 즉, 최소제곱법 기반의 최적화를 한다.

 $ Loss(\vec{w}) = \frac{1}{\lvert D_{train} \rvert} \sum (\vec{w} \cdot \phi(x) - y)^2$ 

 따라서 Loss의 gradient는 다음과 같다.

 $ \triangledown_\vec{w} Loss(\vec{w}) = 2\sum(\vec{w} \cdot \phi(x) - y) \cdot \phi(x) $

Training

 위의 Loss를 최소화하는 방향으로 $\vec{w}$를 최소화 시키기 위해, gradient의 반대 방향으로 $\vec{w}$를 갱신해 주면 된다.

 $ \vec{w} = \vec{w} - \eta\triangledown_\vec{w} Loss(\vec{w}) = \vec{w} - 2\eta\sum(\vec{w} \cdot \phi(x) - y) \cdot \phi(x) $

 여기서 $\eta$는 gradient를 따라 얼마나 이동할 것인지를 정하는 값으로, 너무 작으면 학습이 느리고 너무 크면 너무 크게 움직이며 궤도 밖에서 빙빙 돌 수 있으므로 적절한 값을 정해야 한다.

Python Code

def F(w, data):
    return sum(w.dot(x) - y for x,y in data)/len(data)

def dF(w, data):
    return sum(2*(w.dot(x) - y) * x for x,y in data)/len(data)

def gradient_discent(true_w,data,w):
    eta = 0.01
    for i in range(10000):
        w -= eta * dF(w,sample)

w = np.random.randn(d)
gradient_discent(true_w,sample,w)

 F가 loss값이고, dF가 gradient 값이다. 위의 코드에서 true_w는 정답이 되고, sample은 학습시킬 데이터가 되며, w를 학습시키게 되며, 학습이 진행됨에 따라 w가 true_w값에 가까워진다.

Stochastic Gradient Discent

 위의 GD에서의 gradient는 모든 데이터값의 gradient의 평균이었다면, SGD에서는 각각의 데이터(임의의 선택된 데이터)에 대하여 학습을 진행한다. 얼핏 개개의 데이터에 대하여 학습을 진행하면, 결과가 좋지 않을 것 같지만 많은 경우 SGD가 GD보다 더 좋은 결과를 보여준다. 

 위의 GD의 경우 각 스텝마다 모든 데이터에 대하여 학습하므로 속도가 굉장히 느리다.

SGD에서의 Training

 $ Loss(\vec{w}) = \frac{1}{\lvert D_{train} \rvert} \sum_{(x,y)\in \lvert D \rvert} (\vec{w} \cdot \phi(x) - y)^2$

으로 GD와 같지만,

 모든 $(x,y)$에 대해서 각각 학습을 진행해준다.

 $ \vec{w} = \vec{w} - \eta\triangledown_\vec{w} Loss(\vec{w,y,w}) = \vec{w} - 2\eta(\vec{w} \cdot \phi(x) - y) \cdot \phi(x) $

Python Code

def sF(w,data):
    x,y = data
    return w.dot(x) - y
def sdF(w,data):
    x,y = data
    return w*(w.dot(x)-y)*x
def stochastic_gradient_discent(true_w,data,w):
    eta = 0.03
    for i in range(10000):
        for x, y in data:
            w -= eta*sdF(w,(x,y))

w2 = np.random.rand(d)
stochastic_gradient_discent(true_w,sample,w2)​

* 본 포스트는 Stanford의 CS221 강의를 보고 요약 정리한 것입니다.