Gradient Discent
어떤 함수 $f(x)$가 있을 때, $f(x)$가 최소가 되는 $x$ 값을 찾는 방법으로, $f(x)$의 gradient의 반대방향으로 $x$값을 변화시키는 방법이다. (gradient의 방향이 $f(x)$를 최대화시키는 방향을 나타내는데, 우리는 $f(x)$가 최소가 되는 $x$값을 찾고 싶으므로 반대방향으로 움직여야 한다.)
Linear Regression
Feature $\phi(x)$로 부터 $y$를 예측하는 선형회귀 모델에서 input $x$로부터의 예측값 $f_w(x)$는 다음과 같이 주어진다.
$f_w(x) = \vec{w} \cdot \phi(x)$
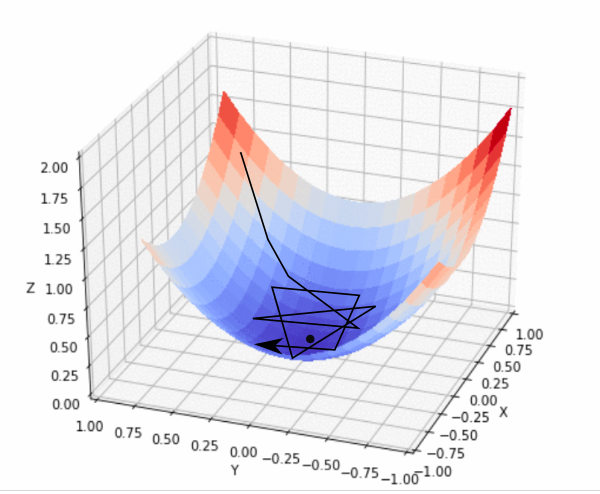
출처 : https://blog.paperspace.com/content/images/2018/05/fastlr.png
위의 그림은, $z$ 값이 $f_w(x)$가 되며, $x$가 2차원으로 $(x,y)$로 주어지는 경우로, 우리는 점이 찍혀있는 $f_w(x)$ 값이 가장 낮은 점의 $(x,y)$값을 찾기를 원하는 것이다.
Loss
본강의에서는 Loss를 위의 예측값과 실제 값 $y$의 차의 제곱, 즉 residual의 제곱으로 한다. 즉, 최소제곱법 기반의 최적화를 한다.
$ Loss(\vec{w}) = \frac{1}{\lvert D_{train} \rvert} \sum (\vec{w} \cdot \phi(x) - y)^2$
따라서 Loss의 gradient는 다음과 같다.
$ \triangledown_\vec{w} Loss(\vec{w}) = 2\sum(\vec{w} \cdot \phi(x) - y) \cdot \phi(x) $
Training
위의 Loss를 최소화하는 방향으로 $\vec{w}$를 최소화 시키기 위해, gradient의 반대 방향으로 $\vec{w}$를 갱신해 주면 된다.
$ \vec{w} = \vec{w} - \eta\triangledown_\vec{w} Loss(\vec{w}) = \vec{w} - 2\eta\sum(\vec{w} \cdot \phi(x) - y) \cdot \phi(x) $
여기서 $\eta$는 gradient를 따라 얼마나 이동할 것인지를 정하는 값으로, 너무 작으면 학습이 느리고 너무 크면 너무 크게 움직이며 궤도 밖에서 빙빙 돌 수 있으므로 적절한 값을 정해야 한다.
Python Code
def F(w, data):
return sum(w.dot(x) - y for x,y in data)/len(data)
def dF(w, data):
return sum(2*(w.dot(x) - y) * x for x,y in data)/len(data)
def gradient_discent(true_w,data,w):
eta = 0.01
for i in range(10000):
w -= eta * dF(w,sample)
w = np.random.randn(d)
gradient_discent(true_w,sample,w)F가 loss값이고, dF가 gradient 값이다. 위의 코드에서 true_w는 정답이 되고, sample은 학습시킬 데이터가 되며, w를 학습시키게 되며, 학습이 진행됨에 따라 w가 true_w값에 가까워진다.
Stochastic Gradient Discent
위의 GD에서의 gradient는 모든 데이터값의 gradient의 평균이었다면, SGD에서는 각각의 데이터(임의의 선택된 데이터)에 대하여 학습을 진행한다. 얼핏 개개의 데이터에 대하여 학습을 진행하면, 결과가 좋지 않을 것 같지만 많은 경우 SGD가 GD보다 더 좋은 결과를 보여준다.
위의 GD의 경우 각 스텝마다 모든 데이터에 대하여 학습하므로 속도가 굉장히 느리다.
SGD에서의 Training
$ Loss(\vec{w}) = \frac{1}{\lvert D_{train} \rvert} \sum_{(x,y)\in \lvert D \rvert} (\vec{w} \cdot \phi(x) - y)^2$
으로 GD와 같지만,
모든 $(x,y)$에 대해서 각각 학습을 진행해준다.
$ \vec{w} = \vec{w} - \eta\triangledown_\vec{w} Loss(\vec{w,y,w}) = \vec{w} - 2\eta(\vec{w} \cdot \phi(x) - y) \cdot \phi(x) $
Python Code
def sF(w,data):
x,y = data
return w.dot(x) - y
def sdF(w,data):
x,y = data
return w*(w.dot(x)-y)*x
def stochastic_gradient_discent(true_w,data,w):
eta = 0.03
for i in range(10000):
for x, y in data:
w -= eta*sdF(w,(x,y))
w2 = np.random.rand(d)
stochastic_gradient_discent(true_w,sample,w2)
* 본 포스트는 Stanford의 CS221 강의를 보고 요약 정리한 것입니다.
'ML > CS221 Stanford' 카테고리의 다른 글
| On-Policy 와 Off-Policy (0) | 2020.03.21 |
|---|---|
| Lecture 9. Game playing 1 (0) | 2020.03.11 |
| Lecture 8: Markov Decision Processes - Reinforcement Learning (0) | 2020.02.27 |
| Lecture 7: Markov Decision Processes - Value Iteration (0) | 2020.02.25 |
| Lecture4 Generalization, K-means (0) | 2020.02.19 |